在硫酸生產(chǎn)過程中，PID作為一種主要的控制策略，被廣泛應(yīng)用于各類控制系統(tǒng)中。它由被控對象、測量變送環(huán)節(jié)、反饋控制器及末端執(zhí)行機(jī)構(gòu)等部分組成。然而，在實(shí)際操作中，許多人對PID整定感到無從下手，這主要?dú)w因于對PID三個參數(shù)的內(nèi)涵及其對控制曲線影響的不熟悉。

本文旨在以簡潔明了的語言解析PID的概念，并通過仿真曲線形式詳細(xì)闡述硫酸化工生產(chǎn)過程中PID三項(xiàng)參數(shù)對整定曲線的具體影響。

1.閾值判斷法的局限

在實(shí)際硫酸生產(chǎn)過程中離不開對溫度、壓力、液位、組分、流量化工五大參數(shù)進(jìn)行控制。本文以溫度控制為例，首先在不加任何控制算法的情況下能想到的是簡單的閾值判斷法來進(jìn)行溫度調(diào)控，當(dāng)溫度大于某個定值溫度時(shí)立馬解除相關(guān)聯(lián)的升溫措施，在理想的安全生產(chǎn)環(huán)境下，會得到一張控制曲線：

圖1.1 閾值控制下的仿真擬合曲線

仿真結(jié)果顯示出上下無規(guī)律的波動，控制器件的靈敏度和加熱性能等因素可能導(dǎo)致其產(chǎn)生振蕩，且難以有效控制。在硫酸生產(chǎn)過程中，由于溫度高且存在變送滯后和熱傳導(dǎo)滯后等問題，閾值控制無法及時(shí)響應(yīng)，振動還會增大。此時(shí)，PID控制的優(yōu)勢便得以凸顯。PID是“Proportion Integration Differentiation”的縮寫，本質(zhì)上是一個公式，由比例項(xiàng)（Proportion）、積分項(xiàng)（Integration）和微分項(xiàng)（Differentiation）三部分構(gòu)成，其具體形式如下所示：

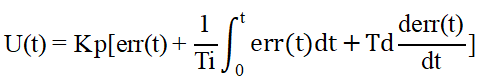
U（t）代表輸出控制量;

Kp表示比例增益；

Ti表示積分時(shí)間 ；

Td表示微分時(shí)間；

err（t）表示的誤差即我們的設(shè)定值（SV）與過程變量（PV）的差值

1.1 比例增益Kp

根據(jù)公式，可以明顯看出，在積分和微分不參與的情況下，PID的kp值實(shí)際上與輸出信號呈線性關(guān)系。假如輸出控制量（閥門開度）的值得范圍在 20%—70%，輸入的err范圍在50-100℃當(dāng)為50℃時(shí)輸出量需要到達(dá)到20%，就需要通過比例系數(shù)來構(gòu)建輸入與輸出的線性關(guān)系。對于kp，其值越大比例作用增大，可以加快調(diào)節(jié)速度，減少誤差，但是過大的比例增益會出現(xiàn)振蕩現(xiàn)象使得系統(tǒng)穩(wěn)定性下降。下方的對比圖可以直觀展示隨著比例增益的不斷增大，會出現(xiàn)何種現(xiàn)象。

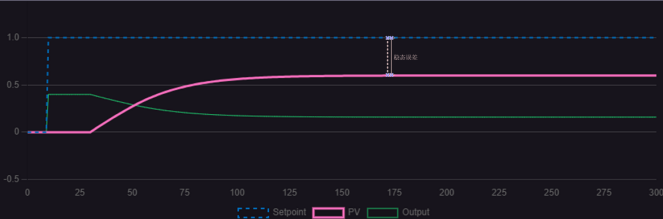
圖1.1.1 Kp比例增益為1

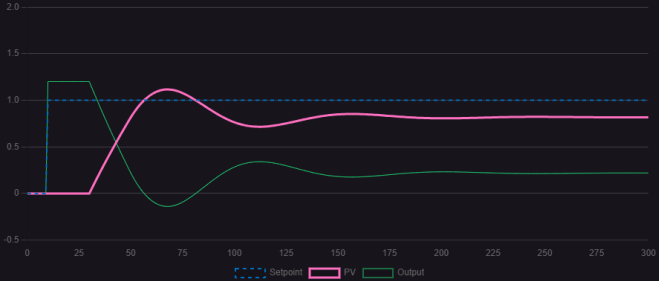
圖 1.1.2 Kp比例增益為3

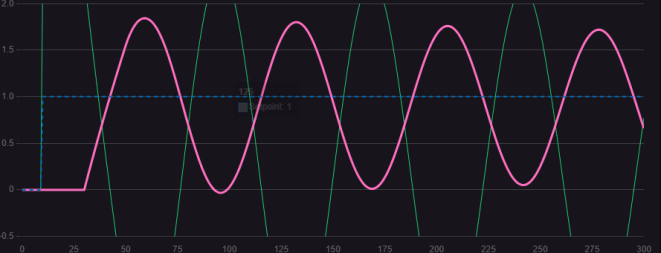
圖 1.1.3 Kp比例增益為5.7

對比三幅控制曲線，合適的Kp值能夠有效加快調(diào)節(jié)速度并消除穩(wěn)態(tài)誤差。過小的Kp值會導(dǎo)致明顯的穩(wěn)態(tài)誤差，而過大的Kp值則會出現(xiàn)等幅振蕩的情況。

1.2 積分時(shí)間Ti

只有比例增益的控制曲線與上文提到的閾值判斷法并無顯著差異，甚至過小或過大的比例增益效果還不如閾值判斷法。在此基礎(chǔ)上，引入積分和微分控制，其中積分系數(shù)對應(yīng)于控制曲線下方的面積，這個面積值代表相應(yīng)時(shí)間段的誤差累計(jì)。將該累計(jì)值乘以系數(shù)進(jìn)行變換后，疊加到輸出上，可在一定程度上消除穩(wěn)態(tài)誤差，提升系統(tǒng)穩(wěn)定性。積分時(shí)間與積分作用成反比。接下來，將展示并分析有比例作用參與的積分控制曲線，探討積分在控制曲線中的具體作用。

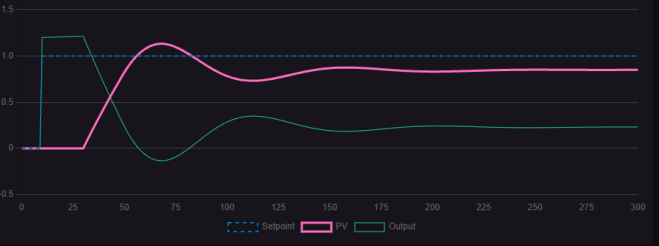
圖1.2.1 P=3 I=0.002時(shí)的控制曲線圖

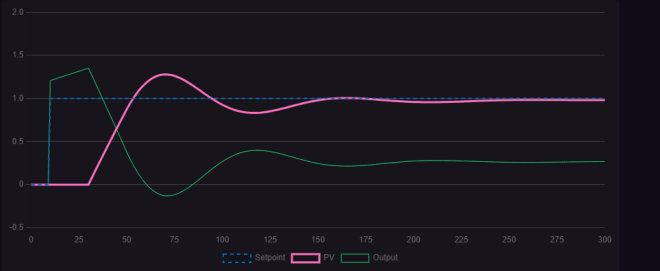
圖1.2.2 P=3 I=0.018時(shí)的控制曲線圖

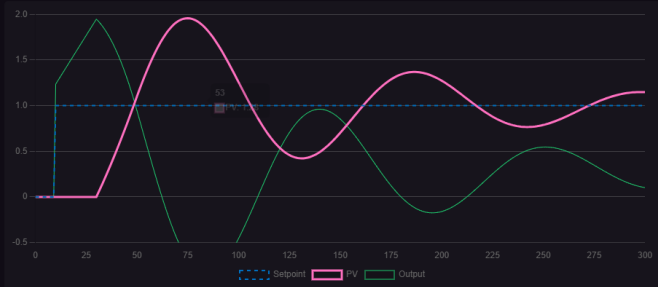
圖1.2.3 P= 3I=0.089時(shí)的控制曲線圖

觀察三幅圖，與僅含比例增益的控制曲線圖相比，較小的積分作用對穩(wěn)態(tài)誤差有一定的消除效果，但并不顯著；隨著積分作用的增強(qiáng)，可以看到控制曲線與目標(biāo)線逐漸重合，穩(wěn)態(tài)誤差基本消除。然而，繼續(xù)加大積分作用，明顯出現(xiàn)衰減振蕩波形，且持續(xù)時(shí)間較長，波形最終仍會趨于目標(biāo)值。因此，積分作用能夠有效消除穩(wěn)態(tài)誤差，但過大的積分作用會導(dǎo)致動態(tài)響應(yīng)變慢，出現(xiàn)長周期的衰減振蕩。在實(shí)際控制過程中，允許過程變量（PV）在一定范圍內(nèi)波動。選擇適當(dāng)?shù)谋壤饔每梢约涌煺{(diào)節(jié)速度，但會伴隨一定的超調(diào)量，需確保該超調(diào)量在生產(chǎn)誤差允許范圍內(nèi)，以實(shí)現(xiàn)控制系統(tǒng)的穩(wěn)定、準(zhǔn)確和快速響應(yīng)。圖1.2.4展示了在適宜比例作用下的控制曲線。

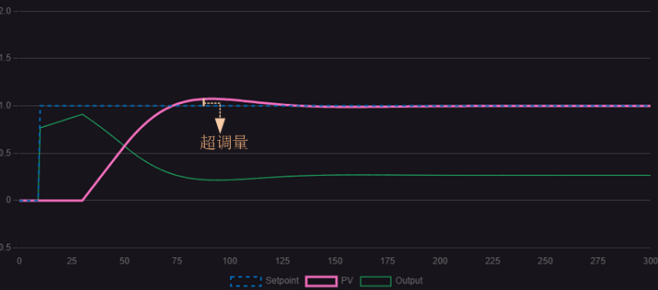
圖1.2.4 P=3 I=0.019

1.3 微分時(shí)間Td

微分的作用在于減少超調(diào)量和縮短調(diào)節(jié)時(shí)間，以下將通過仿真曲線的形式為大家詳細(xì)解釋。

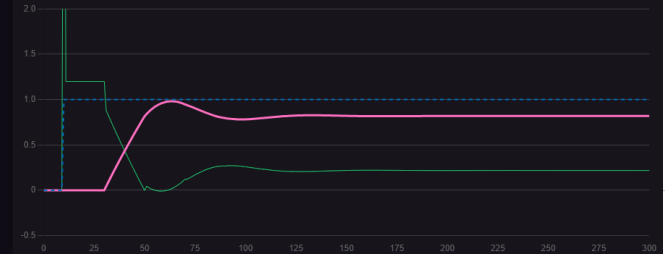
圖1.3.1 P=3 D=12.5

通過圖1.1.2與1.3.1對比，加入微分作用后超調(diào)量和震蕩幅度有明顯的下降，趨于穩(wěn)態(tài)的調(diào)節(jié)時(shí)間也有所縮短。

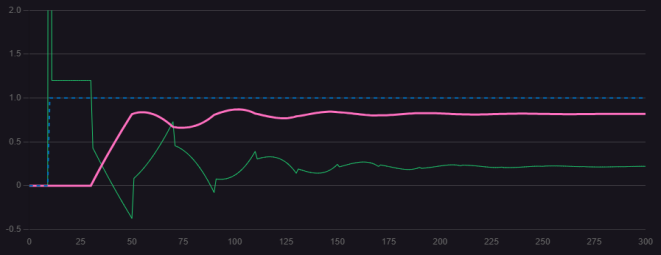
圖1.3.2 P=3 D=40

若增大微分，超調(diào)量將顯著減小，然而不恰當(dāng)?shù)奈⒎肿饔脮?dǎo)致控制曲線出現(xiàn)振蕩，進(jìn)而使穩(wěn)定時(shí)間延長，甚至難以實(shí)現(xiàn)系統(tǒng)穩(wěn)定。

微分作用與積分作用均無法獨(dú)立進(jìn)行控制，亦不能聯(lián)合作用，必須輔以比例作用的參與。

1.4 PID系統(tǒng)調(diào)節(jié)

首先，依據(jù)PI系統(tǒng)進(jìn)行參數(shù)調(diào)節(jié)，先調(diào)整比例系數(shù)P，再調(diào)整積分系數(shù)I，以確保系統(tǒng)具備適量的超調(diào)量并能迅速達(dá)到穩(wěn)定狀態(tài)。同時(shí)，需確保誤差控制在可接受的范圍內(nèi)，且不影響后續(xù)工序或觸發(fā)聯(lián)鎖機(jī)制。具體仿真結(jié)果如下所示：

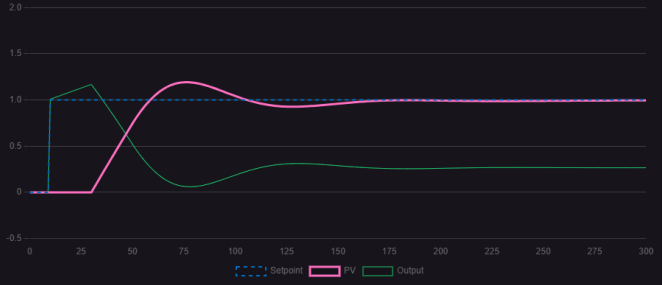
圖1.4.1 PI作用下的整定曲線

在這種情況下慢慢加入微分作用，消除超調(diào)量，進(jìn)一步減少穩(wěn)定時(shí)間。如下圖：

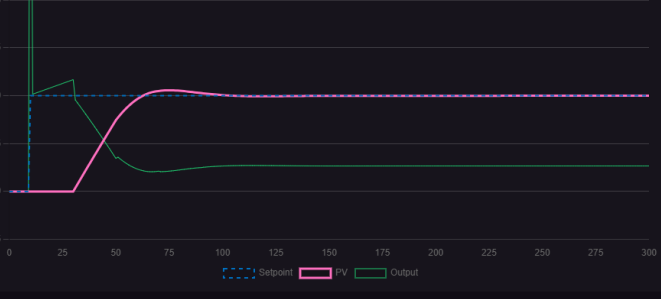
圖1.4.2 PID作用下的整定曲線

通過上圖可以看出，PID控制所得到的曲線相對較為平穩(wěn)。然而，在實(shí)際控制中，通常會將兩種作用相結(jié)合使用。只要誤差在允許范圍內(nèi)，對生產(chǎn)的影響并不顯著，因此一般會采用PI控制。值得注意的是，PI控制在整個化工領(lǐng)域的應(yīng)用比例高達(dá)75%。

Kp、Ti、Td三者相互影響，且整定過程耗時(shí)較長，實(shí)現(xiàn)完美控制頗具挑戰(zhàn)。本文僅對調(diào)試思路進(jìn)行簡要分析，實(shí)際操作中需考慮的因素更為復(fù)雜，包括控制器的選型、單閉環(huán)間的相互干擾、控制系統(tǒng)慣性及滯后效應(yīng)等。